No, you can't. At least that's the conclusion of two key philosophers of digitality, Nelson Goodman and Gottlob Frege. It's impossible to forge the discrete elements of a symbolic system, elements like the letter "A," the number "7," or the truth values "true" and "false."
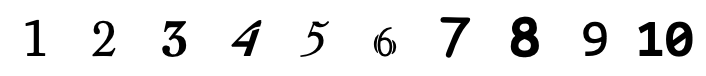
Symbolic expressions like words and sentences can be forged, of course, not to mention paintings which are eminently forgeable. But symbols themselves are unforgeable. Or so claim both Goodman and Frege.
I described Frege previously in a post on "Digital Univocity." Today I'd like to explore Goodman. If Frege approached the question from the perspective of sets and truth values, Goodman's approach was essentially semiotic and graphical. And while they both come to the same conclusion, they do so for quite different reasons. It's worth walking through the argument to see why and how they claim the uniqueness of discrete atoms. This sense of the absolute incorruptibility of the symbolic order gets to the very heart of digital philosophy.
Based on six lectures given at Oxford in 1962, Nelson Goodman's Languages of Art: An Approach to a Theory of Symbols, while ostensibly about "art," approached the topic more from the perspective of semiotics and linguistics than through debates in fine art or aesthetics. The book is essentially a work of epistemology and philosophy of language, which is typical for a mid-century analytic philosopher. Perhaps most notable is the section on what Goodman called the "autographic" and the "allographic" (which I'll gloss in a moment). And, for my purposes, the book is also important because it contains a short section on "Analogs and Digits," one of the earliest examples of theoretical inquiry into the concepts of the analog and the digital. (A few years later in 1971 David Lewis wrote a brief but potent response to Goodman titled "Analog and Digital.")
In the particularly rich part three on "Art and Authenticity," Goodman revealed his obsession with fakes and forgeries. He offered an interesting twist around the question of artistic originality, namely that (1) you can't forge a symphony by Haydn, and (2) you can't make an original Rembrandt (115); "in music, unlike painting, there is no such thing as a forgery of a known work...of the London Symphony...there can be no forgeries" (112). Such grand posturing toward high art -- you can't...you can't -- will likely offend our postmodern ears; people today don't much like proscription, plus we've more or less moved on from the old modern anxieties around authenticity and inauthenticity, be they Heidegger's nostalgia for the peasant's shoes, or Benjamin's observations on aura decay. Nevertheless, Goodman's argument is an interesting one, and quite possibly correct, or at the very least a successful illustration of that particular ideology known as digital philosophy.
Of course an enterprising imposter could pen a new symphony and try to pass it off as an authentic Haydn through mis-attribution. Goodman's argument here was very specific. His argument was not about forging Haydn's hand; rather, Goodman claimed that it's impossible to forge a specific extant work such as the London Symphony. Why? Because reproducing the symphony does not diminish the work. Every iteration of the symphony is as real as any other. Or, as Goodman plainly put it, "last night's performance [is] no less genuine than the premiere" (112).
This sort of "immunity to the less genuine" characterizes an entire class of art works, what Goodman grouped under the label "allographic" art. By contrast, "if the distinction between original and forgery of it is significant" (113), the work shall be labeled "autographic." I've long been fascinated by the allographic/autographic distinction, after first being exposed to it in the context of computer art (where the allographic is particularly prevalent). Coined from the Greek terms meeting "self writing" or "same writing," autographic works are works that are bound to a specific material object. For Goodman these include painting and sculpture. Consider the nature of the signature (the autograph); autographic works don't so much convey the signature of the artist as they do the signature of themselves. The autographic work expresses the uniqueness of itself, and hence can't help but broach questions of source, authenticity, essence, and, by extension, forgery.
By contrast, allographic art -- from the Greek meaning "other writing" or "difference writing" -- are works rooted in a dematerialized essence. (Alas, how such a concept, "dematerialized essence," has been entirely stricken from polite conversation!) Goodman furnished a few examples, some more convincing than others. Music is primary here, but Goodman also mentioned architecture, drama, and poetry. "There is no such thing as a forgery of [Thomas] Gray's Elegy [Written in a Country Churchyard]" (114) he insisted. The question of notation emerges as particularly characteristic of the allographic; something about scripts and symbols pushes a work a bit closer to the status of "difference writing." Or as Goodman put it, "art seems to be allographic just insofar as it is amenable to notation" (121). Such dematerialization into notation, or farther into pure essence, unburdens the allographic from any obligations around authenticity, not because it can't be reproduced but because its own reproduction is immaterial. Goodman's argument is essentially metaphysical: Haydn's London Symphony has the strange quality of there being only one even after multiple reproductions. Why? Because the "original" is already, in a sense, inessential. (Which is not to dispute the existence of a musical score, carefully preserved in the Haydn archives, wherever they may be.) Ironically, once the art work becomes pure essence, purely cast from metaphysical stuff, it gains immunity to questions of authenticity. At 100% authenticity, the question of forgery drops to zero.
But what did Goodman mean to gain with his Haydn reference? And is it a good example? The question of authenticity is at the very least evoked if I try to paint a copy of a Cézanne, or if Vija Celmins reproduces a rock. One can debate the question, pro or con. Artists can make work that probes the limit, dissolving it or reinforcing it. Goodman's point was that the question of authenticity is simply never broached if I sing "Happy Birthday" or dance the tango. Even if I were to eke out a terrible rendition of Haydn on the piano, it might be an insult to the ears but it's certainly not a forgery. Sure there's an archival negative of Citizen Kane in a vault somewhere, but every screening of Welles is as "authentic" as any other. I put the word "authentic" in scare quotes; in fact, the word doesn't have much meaning in the context of allographic art.
These kinds of distinctions typically send artists and art historians into conniption fits. Classifying entire artistic practices as Goodman does -- sculpture is autographic while drama is allographic -- is offensive not only to the spirit of art making, but also to the actual practice of art, which in recent decades has focused with maniacal precision on the disruption of categorical distinction and the suspension of any essential quality of a work, so much so that "working across media" or being "at the intersection of painting and sculpture" are practically required confessionals in any artist's statement today despite being the most banal cliche. And there's something to this; practices like appropriation, the ready-made, reproduction, and mimicry (Elaine Sturtevant, Sherrie Levine, Richard Prince, and other examples too numerous to itemize), not to mention homage, influence, or reinvention -- a Virgil for every Homer -- are practically synonymous with the very meaning of art. Yet, in the spirit of perverse contrarianism, or at least as a kind of base corrective to today's dominant tendencies, I find Goodman's overweening categorizations refreshing.

But what of our starting provocation, that it's impossible to forge the letter "A"? The answer comes a bit later in the book, when Goodman turned to a commentary on alphabetical characters, and specifically what he called character indifference (132). Character indifference simply means that the glyph used to represent a letter (a/a/A/a) doesn't particularly matter at the level of syntax, even if it might have aesthetic or even semantic significance. As Goodman put it, characters "may be freely exchanged for one another without any syntactical effect" (131). The consequence is clear, even if Goodman never had to say it: characters are allographic. And thus if characters are allographic, then, as per the above, the question of authenticity no longer applies. In other words, it's impossible to forge the letter "A." And every "7" is as good as any other.
Difference writing or same writing? The allographic is clearly more fascinating than the autographic. The latter entails materiality, presence, and authenticity. The former fully dematerializes into a kind of generic vernacular, by way of notation and the proliferation of signifiers. Can you forge a nursery rhyme? Can you forge genre? Perhaps not, given an immunity to the less genuine.
+ + +
Postscript -- Let me add two points of criticism concerning Goodman's brief but significant commentary on "Analogs and Digits." Goodman must be commended for investigating these concepts at a relatively early point, and his description is accurate if routine: the analog is continuous, while the digital is discrete. However he gets a few details wrong and I thus diverge from Goodman at both the general and specific levels. Speaking generally, Goodman claimed that "a digital system has nothing special to do with digits, or an analog system with analogy" (160), which is clearly misguided. Digital systems have everything to do with digits, and analog systems have everything to do with analogies. More specifically, I disagree with Goodman's assessment of rational and real numbers, namely his characterization of the analog as "dense." Mathematicians use "dense" to describe the rational number line. I associate rational numbers with the digital paradigm and real numbers with the analog paradigm. By this logic, the analog is not "dense" in the mathematical sense; if anything, density would most aptly characterize the digital instead of the analog. Goodman did not agree however, writing that "the distinction between density or compactness and continuity--between the rational and the real numbers--need not trouble us much here" (136n6). In other words Goodman was aware of mathematicians' use of "dense" to describe rational numbers ("digital" numbers in my parlance), yet he used the term to describe the analog instead.
