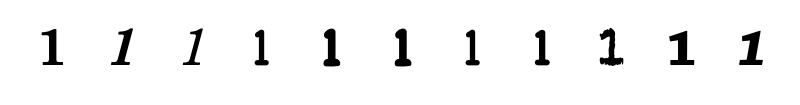 Over the summer I read a lot of Lacan and revisited some influential Lacanian texts including Jacques-Alain Miller's 1966 essay on "Suture" published in the first volume of Cahiers pour l’Analyse. It's an important essay, garnering key responses from Alain Badiou (and, much later, Zizek), as well as helping to spawn a whole cottage industry of Lacanian cinema studies. Curiously, both Miller and Lacan make use of the mathematician and logician Gottlob Frege -- a strange pairing indeed considering how Lacan and Frege are worlds apart, the one a poststructuralist psychoanalyst, the other a logicist and progenitor of what would come to be known as analytic philosophy.
Over the summer I read a lot of Lacan and revisited some influential Lacanian texts including Jacques-Alain Miller's 1966 essay on "Suture" published in the first volume of Cahiers pour l’Analyse. It's an important essay, garnering key responses from Alain Badiou (and, much later, Zizek), as well as helping to spawn a whole cottage industry of Lacanian cinema studies. Curiously, both Miller and Lacan make use of the mathematician and logician Gottlob Frege -- a strange pairing indeed considering how Lacan and Frege are worlds apart, the one a poststructuralist psychoanalyst, the other a logicist and progenitor of what would come to be known as analytic philosophy.
While Lacan jumped around a lot -- he particularly liked the graphical notation scheme Frege unveiled in his Begriffsschrift of 1879, and he borrowed from Frege's quantifier logic for his formulas of sexuation -- Miller himself focused more specifically on Frege's second major treatise The Foundations of Arithmetic (or the so-called Grundlagen) published in 1884. Surprisingly readable for a math text, Frege's Foundations of Arithmetic presents a novel theory of number, different from some of those that came before (namely, Kant, Leibniz, and Mill). Famously, Frege developed a theory of number rooted in pure logic, rather than intuition or empirical experience. He also began with the number zero -- not unimportant, given philosophy's customary interest in, alternately, the one and the many -- rooting zero in (a negation of) the principle of identity.
Frege's seed concept, the negation of the principle of identity, has a cardinality, namely none. If the principle of identity is true for all things, then no things fall under the negation of the principle. And the concept of that absence is, for Frege, a number, the number zero.
Miller took it as symptomatic (and deeply meaningful) that Frege would ground his theory of number in zero, the count of an absence, rather than one or another concept entirely like the infinite or the continuous. The conceptual leap from Frege's zero to Lacan's lack is not too far, yet ultimately a bit clumsy. And I suspect Miller overstated his case in suggesting that Frege provided grounds for locating lack in mathematics or, for that matter, logic. Frege was not negating the principle of identity. Quite the opposite, it's the absolute imperviousness of the principle of identity that made Frege's entire system possible.
So let's revisit Frege's system of number with an eye to "digital univocity," that is, the universal identity of discrete atoms. This gets to the very heart of Frege's digital philosophy.
The essence of Frege's intervention lay in the insight that things may "fall under" or be "extensive" with certain concepts. Hence a certain number of things "fall under" the concept of "days of the week" or "continents in the world," namely seven. Frege generally preferred boolean sentences where things either are the case, or are not the case. He developed clever mechanisms for rewriting sentences so that they could be more felicitously expressed in his preferred logical semantics; this frequently involved moving all the adjectives and qualitative nouns into the predicate, and replacing the verb with something like "is the case." By black-boxing empirical verification in this way, Frege could shoehorn sentences into a digital mechanic of yes or no. ("True or false. There are no further truth-values," he maintained in his influential essay "On Sense and Meaning," endorsing what has come to be known as a cornerstone of digital philosophy.) Does something fall under a concept, yes or no? If yes, then that something contributes unambiguously to the count of the concept.
In other words, for any concept or claim, one could look for all the things that fall under that claim. All those things can be counted, and thus, overall, they represent the count of the claim, its cardinality. The concept of that count is what Frege called number. Here are the three basic steps of the argument as enumerated by Frege:
- a concept or claim F
- the cardinality of F -- i.e. how many things fall under the concept
- the concept of the cardinality of F -- the Number of F, a.k.a. #F
The first level refers to any kind of claim or concept. At the second level, Frege used one-to-one correlation to determine the count or cardinality of things that fall under the initial concept. The third level moves one step more abstract, from the cardinality of the concept to the concept of the cardinality: the concept itself of the number of things that fall under the initial concept F. This concept was number, for Frege, numbers like 5, 7, or 42.
So Frege can generate the number #F corresponding to the count of any claim F. But what is the cardinality of #F itself? Frege's astonishing but necessary answer was that the cardinality of any #F will always be one. There's only one concept of the cardinality of "sets of things that are seven," even if there are lots of things in the world that are seven. This is a dramatic conclusion, and a strong indication of Frege's essential idealism/Platonism.
So while Frege was celebrated by Miller et al. as a thinker of zero, the cardinality of digital atoms scuttles that assumption entirely. The most significant cardinality in Frege was not zero, not by a long shot. All numbers have a cardinality of one. Thus the most significant number in all of Frege was one.
In this sense Frege gives us an alternate conception of univocity. His is not the Deleuzian version of univocity, which is based in analogicity, but a characteristically digital univocity expressed through the solo cardinality of every number.
If the count of every number is one -- one precisely -- then no number can be destroyed, and no number can be diminished through duplication or reproduction. In a sense, it's impossible to forge the number "7." And if letters like "G" are merely proxies for digital atoms like "7," then likewise it's impossible to forge letters, since they too have cardinalities of one.
Perhaps this explains the intractability of digital systems; it's the univocity of digital atoms that makes them so intractable. Their univocity -- always one no matter how many times -- imparts a kind of imperviousness to the symbolic order, and likewise to digital systems more generally (if not also to idealism as a whole).
To be sure, Frege's arguments are only persuasive to those already predisposed to the laws of digital philosophy. Analog philosophers will have been skeptically snickering throughout at the seeming arbitrariness of it all. Analog philosophers will say: of course symbols can be multiple -- how idiotic to think otherwise! (Here "idiotic" is derogatory but also technically accurate, as characteristic of one who endorses the theory of identity.) I wanted to walk through the argument above not to endorse it, merely to explore the ideology of digital philosophy.
In the past I've suggested that digitality can't really be "disrupted," perhaps not even "critiqued." Rather, the best approach to digitality is to suspend it. Reproduction doesn't degrade the digital. But unproduction does. We ought to think more about how to degrow the sufficiency of digital atoms. In other words, what interests me most today is not so much the event of the digital, but the prevent.